| たとえば右図のようなもの (この図は半径が1) 角度Θは時間によって変化する―>
角度は時間の関数 |
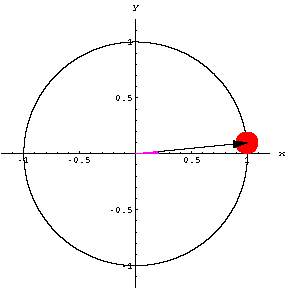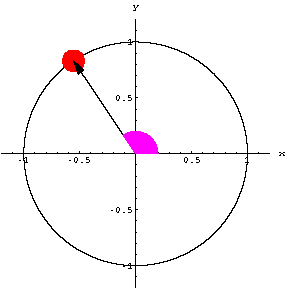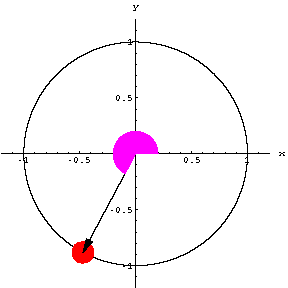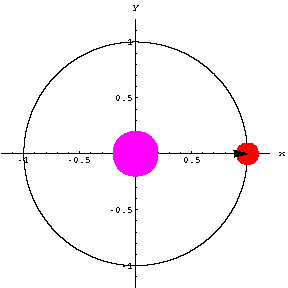 |
物体が原点を中心とした半径 r の円周上を運動している。+ X 軸と物体へひいた位置ベクトルとの間の角を Θとする。回転する速さが一定で、円軌道を描く運動を「等速円運動」と呼ぶ。
| たとえば右図のようなもの (この図は半径が1) 角度Θは時間によって変化する―>
角度は時間の関数 |
 |
角速度―――>単位時間あたりに変化する角度
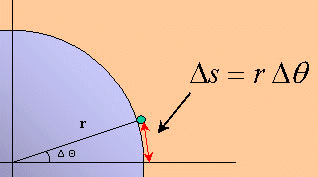
| 回転半径 r のとき、角度⊿Θ
だけ回転した物体が、通った道筋の長さを⊿sとする。そのとき⊿s
は上図から次のように表わされる。
時間 ⊿t の間に、角度が ⊿Θだけ回転するとする。 そのときの角速度 時間 ⊿t の間に物体が進んだ距離は ⊿s だから、物体の速さ v は
|
| 注意 | 角速度 ω が同じでも回転する半径が異なれば物体の速さは異なる。 |
等速円運動と万有引力 3/8