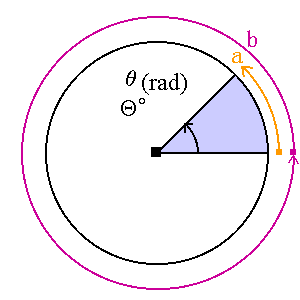
| ●等速円運動 |

角という量を、度“° ”とは異なる目盛り“ラジアン(rad)”ではかる。
| 角の単位 ラジアン: | 一周の角を2πと定めた単位 |
| 角の単位 度 : | 一周の角を360と定めた単位 |
右図より、一周の長さ b と、弧 a の長さの比は、一周の角度に対する弧の角度の比に等しい。
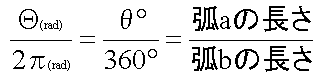 |
| 上式より、弧 a の長さがわかる。 |
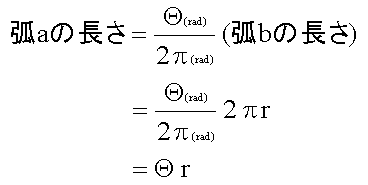 |
ラジアンは(rad)と表されることがあるが、ほとんどの
場合単位名をつけない。
単位名がついていない(“° ”がついていない)角の単位はラジアン
である。
● 度“° ”を使わずにラジアンを使うといいことがあるか?
例えば、右図の弧 x の長さを求めたいとき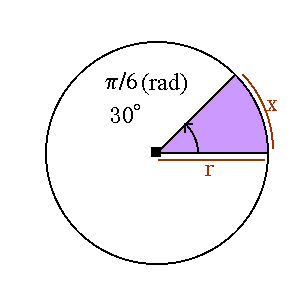
度“° ”の場合 角度360°での弧の長さ=円周=2πr
角度30°での弧の長さ=x (求めたい量)
一周の長さと、弧 x の長さの比は、一周の角度に対する弧の角度の比に等しい。したがって、次式が成立。
30°/360°=x/2πr
この式より、弧の長さがわかる。
x=πr/6
ラジアンの場合 弧の長さ=角(ラジアン)× 半径
x=π/6 r
ラジアンでは弧の長さがすぐにわかる。
例
| 半径rの円の円周の長さは2πr。 このときの中心角は2π(rad) | 半径rの円の半分の弧の長さはπr。 このときの中心角はπ(rad) |
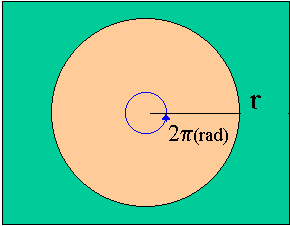 |
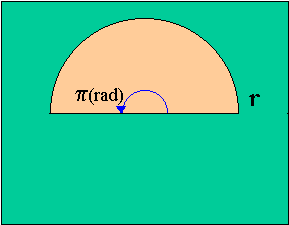 |
| 半径rの円の1/4の部分の弧の長さはπr/2。 このときの中心角はπ/2(rad) | 半径rの円の一部分、中心角θである弧の長さは? θr(rad) |
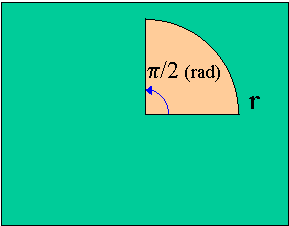 |
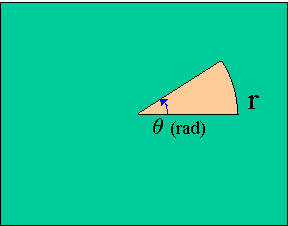 |
等速円運動と万有引力 2/8