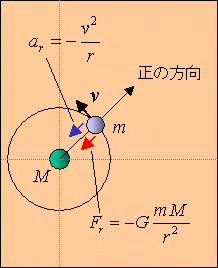万有引力の法則

通常の力学の方法は、物体に加わっている力と運動方程式を前提として、加速度つまり物体の運動を求めてゆく。しかしここでは、物体が等速円運動すると仮定して、運動方程式から導かれる速度と回転半径の間の関係を調べる。

等速円運動をしている物体には中心力が加わっている。この中心力として万有引力を考える。質量ｍの物体が質量 M の物体のまわりを等速円運動している（ M はｍに比べてとても大きい）。このとき質量 m の物体について、半径方向(円の中心から外向きを正とする)の運動方程式は

である。これを変形すると

からとなる。

つまり、等速円運動をしている物体の速さは中心からの距離、回転中心にある物体の質量、万有引力定数だけで決まってしまう。(運動している物体の質量にはよらない)

等速円運動についての説明はこれで終わりです。次は演習問題をやってみましょう。